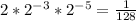Question

Jordan was given the expression 2x2^-3 x 2^-5 How should he write the expression as a fraction? Describe the exponent rules Jordan should use to simplify the expression

Answer 1

`2*2^(-3) * 2^(-5) =(1)/(128)`

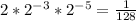
Explanation:

Given

`2*2^(-3) * 2^(-5)`

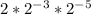
Required

Write as a fraction

To do this, Jordan has to apply the following rules

Negative Exponent rule:

`a^(-m) = (1)/(a^m)`

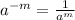
So, the expression is:

`2*2^(-3) * 2^(-5) = (2)/(2^3 * 2^5)`

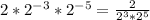
To solve further, we apply the product rule of exponent

`a^m * a^n = a^(m+n)`

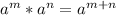
So, the expression is:

`2*2^(-3) * 2^(-5) =(2)/(2^(3+5))`

`2*2^(-3) * 2^(-5) =(2)/(2^8)`

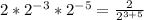
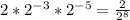
Evaluate the exponents

`2*2^(-3) * 2^(-5) =(2)/(256)`

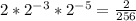
Divide the numerator and denominator by 2

`2*2^(-3) * 2^(-5) =(2/2)/(256/2)`

`2*2^(-3) * 2^(-5) =(1)/(128)`