Question

A student was given the line y=2/3x-1 and the point (-7, 1/2) and asked to find an equation that went through the given point and was perpendicular to the given line. The students answer was y=3/2x+11. Explain what the student did incorrectly the give the correct answer

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, hmmm what's the slope of y=2/3x-1 anyway?

`\bf \begin{array} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}~\hspace{7em}y=\stackrel{\stackrel{m}{\downarrow }}{\cfrac{2}{3}}x-1 \\\\[-0.35em] ~\dotfill`

`\bf \stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{\cfrac{2}{3}}\qquad \qquad \qquad \stackrel{reciprocal}{\cfrac{3}{2}}\qquad \stackrel{negative~reciprocal}{-\cfrac{3}{2}}}`

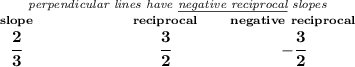
so, notice, "one of his mistakes" is that he used 3/2 as the slope, not -3/2.

so, we're really looking for a line whose slope is -3/2 and runs through (-7, 1/2).

`\bf (\stackrel{x_1}{-7}~,~\stackrel{y_1}{(1)/(2)})~\hspace{10em} slope = m\implies -\cfrac{3}{2} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\cfrac{1}{2}=-\cfrac{3}{2}[x-(-7)]\implies y-\cfrac{1}{2}=-\cfrac{3}{2}(x+7) \\\\\\ y-\cfrac{1}{2}=-\cfrac{3}{2}x-\cfrac{21}{2}\implies y=-\cfrac{3}{2}x-\cfrac{21}{2}+\cfrac{1}{2}\implies y=-\cfrac{3}{2}x-10`