Question

In △ABC, point M is the midpoint of AB , point D∈ AC so that AD:DC=2:5. If AABC=56 yd2, find ABMC, AAMD, and ACMD.

Answer 1

For a better understanding of the solution to this question please go through the diagram in the file that has been attached.

The diagram is made according to the question. We have also done a minor construction in the diagram wherein we have made MP perpendicular to AC. We will need this later.

It has been given that:
`(AD)/(DC)= (2)/(5)`

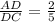
Now, since M is the midpoint, then by definition, CM is the median. We know that a median divides the area of a triangle into two equal parts. Thus, we have:

Area of AMC=Area of BMC=
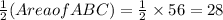`(1)/(2)(Area of ABC)= (1)/(2)* 56=28` squared yards.................(Equation 1)

Therefore the Area of BMC=28
`yd^2`

Now, we know that the remaining other half of the triangle AMC is made up of two triangles, AMD and CMD.

The Area of CMD=
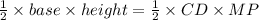`(1)/(2)* base* height= (1)/(2)* CD* MP`.......(Equation 2)

Likewise, The Area of AMD=
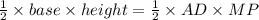`(1)/(2)* base* height= (1)/(2)* AD* MP`.......(Equation 3)

Now, dividing (Equation 3) by (Equation 2) we get:

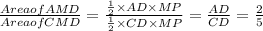`(Area of AMD)/(Area of CMD)=((1)/(2)* AD* MP)/((1)/(2)* CD* MP)= (AD)/(CD)= (2)/(5)`......(Equation 4)

Thus, from the above equation we can see that even the areas are divided in the ratio 2:5.

Therefore, Area of AMD=
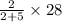`(2)/(2+5)* 28` =8 squared yards.

And hence, the Area of CMD will be the remaining area which is: 28-8=20 squared yards.

Answer 2

Since point M is the midpoint of AB, then AM=MB.

Consider the area of the triangles ABC and BMC:

`A_(ABC)=(1)/(2)\cdot AB\cdot h_c=56\ yd^2,`

where
`h_c` is the height drawn from the vertex C to the side AB.

So,
`AB\cdot h_c=112\ yd^2.`

Now

`A_(BMC)=(1)/(2)\cdot BM\cdot h_c=(1)/(2)\cdot (AB)/(2)\cdot h_c=(1)/(4)\cdot AB\cdot h_c=(1)/(4)\cdot 112=28\ yd^2.`

Also

`A_(AMC)=A_(ABC)-A_(BMC)=56-28=28\ yd^2.`

Now consider the area of the triangles AMD and CMD. Let
`h_M` be the height drawn from the point M to the side AC.

`A_(AMD)=(1)/(2)\cdot AD\cdot h_M=(1)/(2)\cdot (2AC)/(7)\cdot h_M=(2)/(7)\cdot \left((1)/(2)\cdot AC\cdot h_M\right)=(2)/(7)\cdot A_(AMC)=(2)/(7)\cdot 28=8\ yd^2.`

Therefore,

`A_(MDC)=A_(AMC)-A_(AMD)=28-8=20\ yd^2.`

Answer:
`A_(MBC)=28\ yd^2, A_(AMD)=8\ yd^2, A_(MDC)=20\ yd^2.`