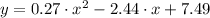Question

Determine the quadratic regression for the data.

(1,5) (3,4) (4,1) (5,2) (7,4)
Explain how you got your answers. Round to the nearest hundredth.

Answer 1

{ solution is attached below}

Answer 2

`y = 0.27\cdot x^(2) - 2.44\cdot x + 7.49`

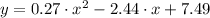
Step-by-step explanation: The quadratic regression is given by :

`y = a\cdot x^(2) +b\cdot x + c`

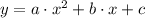
In order to get the quadratic regression equation we need to simplify :

`a\cdot \sum {x_i}^(4)+b\cdot \sum {x_i}^(3)+c\cdot \sum {x_i}^(2)=\sum {x_(i)}^(2)\cdot y_(i)\\a\cdot \sum {x_i}^(3)+b\cdot \sum {x_i}^(2)+c\cdot \sum {x_i}=\sum {x_(i)}\cdot y_(i)\\a\cdot \sum {x_i}^(2)+b\cdot \sum {x_i}+c\cdot {n_i}=\sum y_(i)`

⇒

`3364\cdot a+560\cdot b+100\cdot c=303\\560\cdot a +100\cdot b+20\cdot c=59\\100\cdot a +20\cdot b +5\cdot c=16`

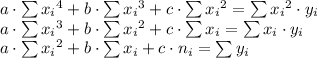
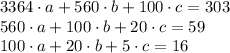
On solving this system of equation, we get a = 0.27 , b = - 2.44 , c = 7.49

Hence, the required quadratic regression is
`y = 0.27\cdot x^(2) - 2.44\cdot x + 7.49`