Given:
Mean height of women in a country (ages 20 -29) i.e,
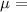 64.1 inches.
64.1 inches.
and the random sample of women in this age group is selected, n = 70
Standard deviation(
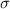 ) =2.93.
) =2.93.
As the relationship between the standard error and the standard deviation is such that, the standard error is equals the standard deviation divided by the square root of the sample size.
Standard Error =
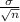
Therefore,
Standard Error(S.E) =

Probability for the mean height for the sample greater than 65 inches,
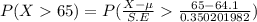 or
or
Let Z=
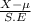
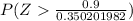 or
or
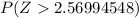 or
or
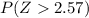
Using Standard Normal Probability table to find the value of
 . i.e,
. i.e,
 = 0.9949
= 0.9949
then,
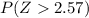 =
=
 = 1-0.9949 =0.0051.
= 1-0.9949 =0.0051.
therefore, the probability that the mean height for the sample is greater than 65 inches is, 0.0051.