Answer:
- A sales person must sell 10 stereos to earn the same salary with each plan.
- A sales person must sell more than 10 stereos to Plan B be better.
- A sales person must sell less than 10 stereos to Plan A be better.
Explanation:
According to the problem.
Plan A:
$250 per week.
$25 per stereo sold.
It's expressed as:
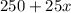
Plan B:
No salary.
$50 per stereo sold.
It's expressed as:
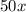
Now, to make the same amount of money with both plans we must solve the following equality
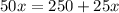
Then, we solve for


So, a sales person must sell 10 stereos to earn the same salary with each plan.
On the other hand, if plan B is better than plan A, it means the following inequality is true
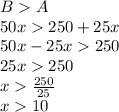
Therefore, if a salesperson sells more than 10 stereos, then the Plan B is better.
If plan A is better, then the following relation is true.

Therefore, if a sales person sells less than 10 stereos, then Plan A is better than Plan B.