Question

What is the slope of the line that passes through the points (-3, 5) and (1, 7)?

1/2
1
2

Answer 1

`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{7}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{7-5}{1-(-3)}\implies \cfrac{7-5}{1+3}\implies \cfrac{2}{4}\implies \cfrac{1}{2}`

Answer 2

The slope the line that passes through the given points (-3, 5) and (1, 7) is 1/2. Hence first option is correct

Solution:

Given, two points are (-3, 5) and (1, 7)

We have to find the slope of a line that passes through the above given two points.

We know that, slope of a line that pass through
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right) \text { and }\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)` is given by:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

Here, in our problem,
`x_(1)=-3, y_(1)=5 \text { and } x_(2)=1, y_(2)=7`

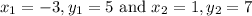
Now, slope m
`=(7-5)/(1-(-3))=(2)/(1+3)=(2)/(4)=(1)/(2)`

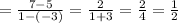
Hence, the slope the line that passes through the given points is 1/2. So, first option is correct.