Question

In NLM, M=(4x-4), L=(3x+12) and N=(6x+3). What is X?
A. 9
B. 12
C. 13
D. 14

Answer 1

The value of x in NLM is 13.

Explanation:

We have a triangle NLM where,

angle M=(4x-4),

angle L=(3x+12); and

angle N=(6x+3).

We know that the sum of angles of a triangle = 180° so we will add these angles and put them equal to 180 to solve for x:

`(4x-4) + (3x+12)+(6x+3)=180`

`4x+3x+6x+12+3-4=180`

`13x=180-11`

`13x=169`

`x=13`

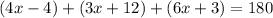
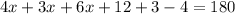
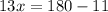
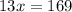
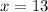
Therefore, the value of x in triangle NLM is equal to 13.