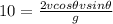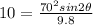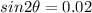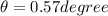Here range of the arrow where it will hit the target is given as
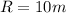
now the vertical displacement of the arrow for whole motion is ZERO
so we will have
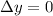
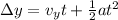
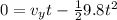
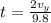
now in the above time it will hit the target at horizontal distance of R = 10 m
so we will have
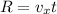
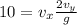
now we know that
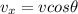
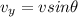
now we will have