9)
we know there are 5 gals, and 6 boys, and "some" adults, let's say there are "x" adults.
so our sample space, namely the total possible outcomes is, 5 + 6 + x, namely 11 + x.
what is the probability that a girl will be picked?
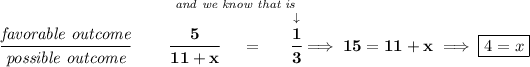
so the sample space is really 5+6+4 = 15.
what is the probability of picking an adult?
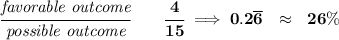
10)
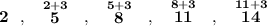
so, as we can see, the common difference is 3, and the first term is of course 2.
![\bf n^(th)\textit{ term of an arithmetic sequence} \\\\ a_n=a_1+(n-1)d\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ d=\textit{common difference}\\[-0.5em] \hrulefill\\ a_1=2\\ d=3 \end{cases} \\\\\\ a_n=2+(n-1)3\implies a_n=2+3n-3\implies a_n=3n-1](https://img.qammunity.org/2019/formulas/mathematics/middle-school/nj10hnrz69qwewj8j8plv295uigqs7nqsb.png)