Question

I need help to doing this problem, please help

Answer 1

9)

we know there are 5 gals, and 6 boys, and "some" adults, let's say there are "x" adults.

so our sample space, namely the total possible outcomes is, 5 + 6 + x, namely 11 + x.

what is the probability that a girl will be picked?

`\bf \cfrac{\textit{favorable outcome}}{\textit{possible outcome}}\qquad \stackrel{\textit{and we know that is}}{\cfrac{5}{11+x}~~~~=~~~~\stackrel{\downarrow }{\cfrac{1}{3}}}\implies 15=11+x\implies \boxed{4=x}`

so the sample space is really 5+6+4 = 15.

what is the probability of picking an adult?

`\bf \cfrac{\textit{favorable outcome}}{\textit{possible outcome}}\qquad \cfrac{4}{15}\implies 0.2\overline{6}~~\approx~~26\%`

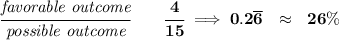
10)

`\bf 2~~,~~\stackrel{2+3}{5}~~,~~\stackrel{5+3}{8}~~,~~\stackrel{8+3}{11}~~,~~\stackrel{11+3}{14}`

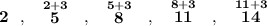
so, as we can see, the common difference is 3, and the first term is of course 2.

`\bf n^(th)\textit{ term of an arithmetic sequence} \\\\ a_n=a_1+(n-1)d\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ d=\textit{common difference}\\[-0.5em] \hrulefill\\ a_1=2\\ d=3 \end{cases} \\\\\\ a_n=2+(n-1)3\implies a_n=2+3n-3\implies a_n=3n-1`

Answer 2

9. 1/7

10. n+3