Question

In isosceles triangle △ABC,

AC
is the base and
AD
is the angle bisector of ∠A. What are the measures of the angles of this triangle if m∠ADB = 110°?

Answer 1

Isosceles triangle:

* two sides are equal.

* the base angle are always equal and

* the altitude is a perpendicular distance from the vertex to the base.

Since, the triangle ABC is an isosceles and AC is the base

⇒ AB=BC and
`\angle A = \angle C`

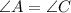
Also, AD is the angle bisector of
`\angle A`, which implies that it cuts the angle at A in two equal halves,

let
`\angle A= x^(\circ)`, then the bisectors cuts it in
`(x/2)^(\circ)`.

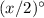As per the given information, we know
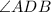`\angle ADB` is 110°, therefore, the line BDC forms a supplementary angle;

⇒
`\angle CDA = 180-110 =70^(\circ)`

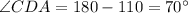
As shown in picture given below:

By sum of all interior angles in a triangle is 180 degree, thus

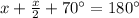`x+(x)/(2) +70^(\circ) =180^(\circ)` or

`(3x)/(2) = 180-70 = 110^(\circ)`

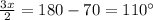
Simplify:

`x=(220)/(3) = 73(1)/(3)^(\circ)`

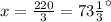
Therefore, the
`\angle A =\angle C = 73(1)/(3)^(\circ)`.

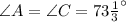Now, to find the angle B, we have;

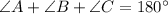`\angle A+ \angle B +\angle C = 180^(\circ)` [Sum of the measure of the angles in a triangle is 180 degree]

or

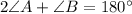`2\angle A+\angle B = 180^(\circ)` or

`\angle B = 180^(\circ)- 2\cdot (220)/(3) =180^(\circ)-(440)/(3)`

Simplify:

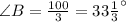`\angle B = (100)/(3)= 33 (1)/(3)^(\circ)`.