Answer: Hence, the length of sides will be 3.2 in, 4.8 in., 6.4 in.
Step-by-step explanation:
Since we have given that
Ratio of lengths of the sides of ΔABC is 2:3:4
So, the length of first side 'AB' be 2x
Length of second side 'BC' be 3x
Length of third side 'AC' be 4x
Now, we have given that M,N,K are the midpoints of the sides ,
As shown in the figure below:
As we know the Mid-point theorem which states that the line joining the midpoints is always parallel to the third side and half to the third side too.
So by applying this we get,
Length of MN is given by
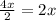
Length of NK is given by

Length of MK is given by
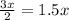
Also, we have given that perimeter of ΔMNK is 7.2 in.
So,
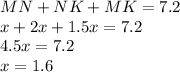
So, the length of AB is given by
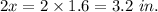
Length of AC is given by
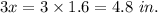
Length of BC is given by
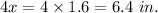
Hence, the length of sides will be 3.2 in, 4.8 in., 6.4 in.