Question

The area ,A of a rectangle is 120x2+78x-90and the length I , if the rectangle is 12x+15 which of the following gives the width w of the rectangle

A. 9x+4
B.10x-19
C.10x-6
D.8x-6

Answer 1

100% sure it is 10x-6

Hope it helps!

Answer 2

Answer: The correct width is given by (C) 10x - 6.

Step-by-step explanation: Given that the area 'A' and the length 'l' of a rectangle r as follows:

`A=120x^2+78x-90,\\\\l=12x+15.`

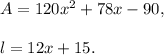
We are to find the width, 'w' of the rectangle.

The AREA of a rectangle is equal to the product of its length and breadth.

So, in the given rectangle, we have

`A=l* w\\\\\Rightarrow w=(A)/(l).`

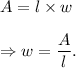
Therefore, the width is given by the quotient of the area and the length of the rectangle.

The width can be calculated as follows:

`w\\\\=(A)/(l)\\\\=(120x^2+78x-90)/(12x+15)\\\\\\=(10x(12x+15)-6(10x+15))/(12x+15)\\\\\\=((10x-6)(12x+15))/((12x+15))\\\\=10x-6.`

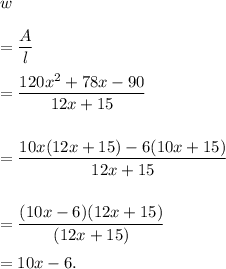
Therefore, width of the rectangle, w = 10x - 6.