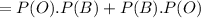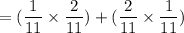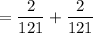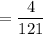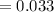Question

1. A bag contains the letters of the word “PROBABILITY”.

If two tiles are chosen (with replacement) what is the probability of choosing an “O” and a “B”?

Answer 1

The probability of drawing an O and a B is 0.033

Solution-

Total number of letter in the word “PROBABILITY” is 11

Total number of B in the word is 2

Total number of O in the word is 1

So, as the tiles are chosen with replacement,

`P(B)=(2)/(11),\ P(O)=(1)/(11)`

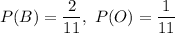
Now, as two tiles are drawn, so the probability of choosing an “O” and a “B” is,

`=P(O).P(B)+P(B).P(O)`

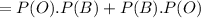
Putting the values,

`=P(O).P(B)+P(B).P(O)`

`=((1)/(11)* (2)/(11))+((2)/(11)* (1)/(11))`

`=(2)/(121)+(2)/(121)`

`=(4)/(121)`

`=0.033`