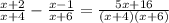Question

I need help with this​

Answer 1

We conclude that:

`(x+2)/(x+4)-(x-1)/(x+6)=(5x+16)/(\left(x+4\right)\left(x+6\right))`

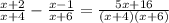
Explanation:

Given the expression

`(x+2)/(x+4)-(x-1)/(x+6)`

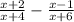
Least Common Multiple of x+4, x+6: (x+4) (x+6)

Adjusting fractions based on the LCM

`=(\left(x+2\right)\left(x+6\right))/(\left(x+4\right)\left(x+6\right))-(\left(x-1\right)\left(x+4\right))/(\left(x+6\right)\left(x+4\right))`

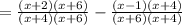
since the denominators are equal, combine the fractions:

`(a)/(c)\pm (b)/(c)=(a\pm \:b)/(c)`

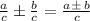
so the expression becomes

`=(\left(x+2\right)\left(x+6\right)-\left(x-1\right)\left(x+4\right))/(\left(x+4\right)\left(x+6\right))`

`=(x^2+8x+12-\left(x-1\right)\left(x+4\right))/(\left(x+4\right)\left(x+6\right))`

`=(x^2+8x+12-x^2-3x+4)/(\left(x+4\right)\left(x+6\right))`

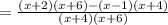
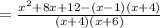
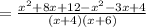
simplify

`=(5x+16)/(\left(x+4\right)\left(x+6\right))`

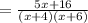
Therefore, we conclude that:

`(x+2)/(x+4)-(x-1)/(x+6)=(5x+16)/(\left(x+4\right)\left(x+6\right))`