Answer:
The correct answer option is h(f(x)) = 2x - 11
Explanation:
We are given two functions:
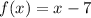 and
and
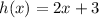
and we supposed to find another function which is
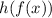 .
.
To find
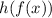 , we need to substitute the value of
, we need to substitute the value of
 in the other function i.e.
in the other function i.e.
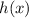 to get:
to get:
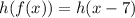
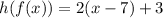
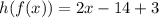
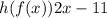
Therefore, the correct answer is h(f(x)) = 2x - 11.