Answer:
All real numbers greater than 1
Explanation:
The domain of a function is the set of possible values in which we can evaluate the function. In other words, it is the possible set of values for x in the expression of the function.
The function is :
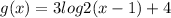
The only restriction in the domain of the function g(x) is given by the logarithm in the function.
The argument of the logarithm function must be greater than 0.
Given a logarithm function
 the expression b is called the argument ⇒ In this exercise we need
the expression b is called the argument ⇒ In this exercise we need
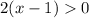
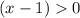
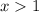
There isn't another restriction for the logarithm inside g(x) ⇒
The domain of g(x) is all real numbers greater than 1.