Question

What is the domain of the function g(x)=3log2(x−1)+4 ?
All real numbers greater than ___

Answer 1

All real numbers greater than 1

Explanation:

The domain of a function is the set of possible values in which we can evaluate the function. In other words, it is the possible set of values for x in the expression of the function.

The function is :

`g(x)=3log2(x-1)+4`

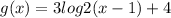
The only restriction in the domain of the function g(x) is given by the logarithm in the function.

The argument of the logarithm function must be greater than 0.

Given a logarithm function
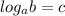`log_(a)b=c` the expression b is called the argument ⇒ In this exercise we need

`2(x-1)>0`

`(x-1)>0`

`x>1`

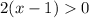
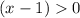
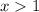
There isn't another restriction for the logarithm inside g(x) ⇒

The domain of g(x) is all real numbers greater than 1.

Answer 2

The domain of
`g(x)=3\log 2(x-1)+4` is,

`\boxed{\boxed{(x:x\ \epsilon\ R\ and\ R>1)}}`

Solution-

For
`y=\log x`, there can not have a log to any value of x, which is either negative or 0.

So domain of log x is,

`(x:x\ \epsilon\ R\ and\ R>0)`

Equating 2(x-1) to 0, we can get the domain of the given function, hence

`\Rightarrow 2(x-1)>0\\\\\Rightarrow x-1>0\\\\\Rightarrow x>1`

Therefore, domain of g(x) is any real number greater than 1, i.e

`(x:x\ \epsilon\ R\ and\ R>1)`