Question

The figure is made up of two cones and a cylinder. Both cones and the cylinder have a 10 mm diameter.

What is the exact volume of this figure?

What is the volume of this figure?


250π mm³

400π mm³

625π mm³

2500π mm³

Answer 1

Answer: 625π mm³

.

Explanation:

Volume of cone =
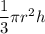`(1)/(3)\pi r^2h` , where r is radius and h is height of cone.

Volume of cylinder =
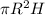`\pi R^2H`, where R is radius and H is height of cone.

For given picture,

Diameter of cone and cylinder = 10 mm , then radius = 5 mm (half of diameter)

h= 15 mm , r= 5mm

R= 5mm , H=15mm

Combined volume of figure = 2 x (Volume of cone)+ Volume of cylinder

`=2*((1)/(3)\pi (5)^2(15))+\pi (5)^2(15)\\\\=250\pi+375\pi\\\\=625\pi\ mm^3`

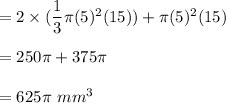
Hence, the volume of this figure is 625π mm³

.

Answer 2

`625\pi\ mm^(3)`

Explanation:

we know that

The volume of the figure is equal to the volume of two cones plus the volume of the cylinder

Find the volume of one cone

`V=(1)/(3)\pi r^(2) h`

we have

`r=10/2=5\ mm` -----> the radius is half the diameter

`h=15\ mm`

substitute the values

`V=(1)/(3)\pi (5^(2))(15)=125\pi\ mm^(3)`

Find the volume of the cylinder

`V=\pi r^(2) h`

we have

`r=10/2=5\ mm` -----> the radius is half the diameter

`h=15\ mm`

substitute the values

`V=\pi (5^(2))(15)=375\pi\ mm^(3)`

Find the volume of the figure

`2*125\pi\ mm^(3)+375\pi\ mm^(3)=625\pi\ mm^(3)`