Answer:
B) Multiply the second equation by −3 to get −3x − 12y = −48
Explanation:
We are given two equations:
 --- (i)
--- (i)
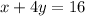 --- (ii)
--- (ii)
If we multiply the second equation by -3, we get:

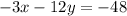 --- (iii)
--- (iii)
Combining equation (i) and (iii) to get:

3x and -3x cancel each other so x is eliminated and we are left with:

Therefore, the correct answer option is B) Multiply the second equation by −3 to get −3x − 12y = −48.