Question

A rectangle is 12 cm long and 9 cm wide. Its diagonal is labeled 2x - 11. What is the value of x?

Answer 1

Answer: 13

Step-by-step explanation:

Use Pythagorean Theorem to find the length of the diagonal (aka hypotenuse) which is also equal to 2x - 11.

12² + 9² = hypotenuse²

144 + 81 = hypotenuse²

144 + 81 = (2x - 11)²

225 = (2x - 11)²

√225 = √(2x - 11)²

15 = 2x - 11

+11 +11

26 = 2x

÷2 ÷2

13 = x

Answer 2

Answer: The value of x is 13 cm.

Step-by-step explanation:

It is given that the length and width of the rectangle are 12 cm and 9 cm.

Use pythagoras to find the value of the diagonal.

`Hypotenuse=√((base)^2+(perpendicular)^2)`

`D=√((12)^2+(9)^2)`

`D=√(144+81)`

`D=√(225)`

`D=15`

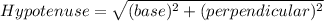
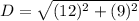
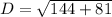
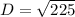
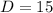
It is given that the diagonal is labeled as 2x-11.

`2x-11=15`

`2x=15+11`

`2x=26`

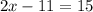
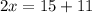
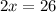
Divide both side by 2.

`x=13`

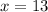
Therefore, x = 13cm.