Factors of 6 are : 1,2,3 and 6.
Let us find probability of getting the number that is a factor of 6.

Now let us find probability of getting a number more than 2 (3,4,5,6).

We can see that these two events are mutually inclusive events. We can find probability of mutually inclusive events by formula
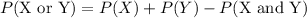 .
.
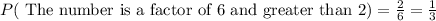
Now we will find probability of getting the number is a factor of 6 or more than 2 using above formula.
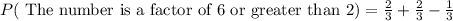

Therefore, our probability will be 1 and this scenario represents mutually inclusive events.