Question

the weight of a bass varies jointly as the girth and the square of its length. a prize winning bass weighed in at 20.4 lb and measured 35 in long with a 22in girth. how much would a bass 32 in long and a 20 in girth weigh

Answer 1

Find out the how much would a bass 32 in long and a 20 in girth weigh .

To proof

As given

weight of a bass varies jointly as the girth and the square of its length

Formula

`w \propto g\ l^(2)`

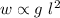
w = k g l²

Where w = weight , g = girth , l = length

k = constant of proportionality

As given

a prize winning bass weighed in at 20.4 lb and measured 35 in long with a 22in girth.

Put all the value in the above equation

we get

20 .4 = k × 35 × 35× 22

`k = (20.4)/(26950)`

k = 0.000757 ( approx )

As given

a bass 32 in long and a 20 in girth weigh

put in the formula

w = 0.000757 × 32 ×32 ×20

w = 15.50 lb( approx)

the weight is 15.50 lb( approx) for a bass 32 in long and a 20 in girth weigh

Hence proved