Answer:
UY = 14
Explanation:
- The median of a triangle is the segment that joins a vertex and the midpoint of the side opposite to this vertex.
- The point of intersection of the medians of a triangle, divide each median at ratio 2: 1 from the vertex
In the given figure
∵ TUV is a triangle
∵ UZ, VX, and TW are medians
∵ UZ ∩ VX ∩ TW at point Y
∴ Y is the point of intersection of the 3 medians
→ By using the 2nd rule above
∵ The point Y divide UZ at the ratio of 2: 1 from the vertex U
∴ UY: YZ = 2: 1
∴
 =
=
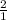
→ By using cross multiplication
∵ UY × 1 = YZ × 2
∴ UY = 2YZ
∵ UZ = UY + YZ
∴ UZ = 2 + 1 = 3 parts
∵ UY = 2 parts
∴
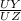 =
=

→ Multiply both sides by UZ
∴ UY =
 UZ
UZ
∵ UZ = 21
∴ UY =
 (21)
(21)
∴ UY = 14