Question

Dario bakes a lasagna containing $\frac 23$ pound of parmesan cheese, $1\frac 14$ pounds of ricotta cheese, and $1\frac 13$ pounds of mozzarella cheese. Dario cuts the lasagna into several equal slices, each containing exactly $\frac 14$ pound of cheeses (of all types totaled). How many slices are there?

Answer 1

Explanation:

First, we compute the total amount of cheese in the lasagna. This is

$$\frac 23 + 1\frac 14 + 1\frac 13 \text{ pounds}.$$We note that $\frac 23+1\frac 13 = 2,$ so the total cheese is equal to $2+1\frac 14 = 3\frac 14$ pounds. As a fraction, this is equal to

$$\frac {12}4 + \frac 14 = \frac{13}4.$$Since each slice contains $\frac 14$ pound of cheese, and $\frac 14\cdot 13 = \frac{13}4$, the total number of slices is $\boxed{13}$.

Answer 2

Answer: There are 13 slices when Dario cuts .

Explanation :

Since we have given that

Quantity of parmesan cheese is given by

`(2)/(3)`

Quantity of ricotta cheese is given by

`1(1)/(4)`

Quantity of mozzarella cheese is given by

`1(1)/(3)`

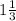
Now, total quantity of cheese Dario have

`(2)/(3)+(5)/(4)+(4)/(3)=2+(5)/(4)=(8+5)/(4)=(13)/(4)`

Now,

According to question, Dario cuts the lasagna into several equal slices and each containing exactly

`(1)/(4)\ pounds\ of\ cheese`

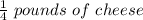
So,

Number of slices is given by

`((13)/(4))/((1)/(4))=13`

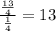
Hence, there are 13 slices when Dario cuts .