Question

Circle N shows tangents ML and MJ intersecting to form LMJ. Find the value of x

A= x=90
B= x=135
C= x=108
D= x=225

Answer 1

B.

Explanation:

Answer 2

We have been given that circle N shows tangents ML and MJ intersecting to form LMJ and measure of angle M is 45 degrees. We are asked to find measure of minor arc length.

Since we know that measure of tangent-tangent angle and measure of minor arc are supplementary.

Let us find measure of our minor arc JL which measures x degrees.

`\angle LMJ+x^(o)=180^(o)`

`45^(o)+x^(o)=180^(o)`

`x^(o)=180^(o)-45^(o)`

`x^(o)=135^(o)`

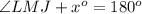
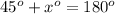
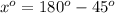
We can see that measure of minor arc is 135 degrees, therefore, option B is the correct choice.