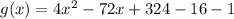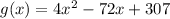Answer:
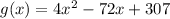
Explanation: to shift a function to the right, we need to subtract as many units as we want to shift from the x (internal function), so if we want to shift the function 9 units to the right, we subtract 9 from the x. To shift a funtion down we need to subtract as many units as we want from the whole function (external function), so in order to shift the function 1 unit down, we subtract 1 from the function:
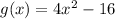
shifting to the right:
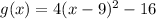
shifting down:
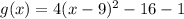
solving the square and the products: