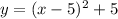We are given parabola equation y=x^2-10x+30.
We need to convert it in vertex form y= a(x-h)^2+k.
We need to find the value of a, h and k to get the vertex form.
For the given equation y=x^2-10x+30, the coefficient of x^2 is 1.
Therefore, a=1.
Now, let us find values of h and k.
h = -b/2a.
h = -(-10)/2(1) = 5.
Plugging x=5 in given equation to get the value of k.
y= x^2-10x+30 => (5)^2 -10(5) +30 = 25 -50 +30 = 5.
Therefore, k =5.
Therefore, vertex (h,k) = (5,5).
So, the vertex form is