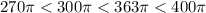Answer-
Solution-
The volume of the cone is given by,
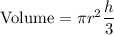
Where,
r = radius of the base circle,
h = height of the cone.
1. Cone with a diameter of 20 units and a height of 12 units
Here,
Radius = 20/2 = 10 units
Height = 12 units
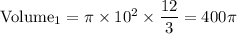
2. Cone with a diameter of 18 units and a height of 10 units
Here,
Radius = 18/2 = 9 units
Height = 10 units

3. Cone with a radius of 10 units and a height of 9 units
Here,
Radius = 10 units
Height = 9 units
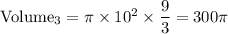
4. Cone with a radius of 11 units and a height of 9 units
Here,
Radius = 11 units
Height = 9 units
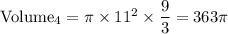
As,