Answer:
Independent
Explanation:
We need to find whether the system of equations
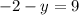 and
and
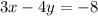 are independent, dependent, or inconsistent.
are independent, dependent, or inconsistent.
Now, we know that the general form of a linear equation in two variables is
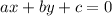
So, the general form of the given equations is
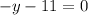 and
and
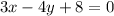
Now, for a system of equations
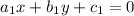 and
and
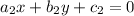 , we need to find
, we need to find
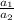 ,
,
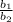 , and
, and
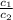
Now,
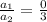
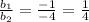
So, we have
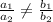
Hence, the system of equations are independent.