Question

The annual rate of depreciation, x, on a car that was purchased for $9,000 and is worth $4,500 after 5 years can be found using the following equation: Graph a system of equations to approximate the value of x, the rate of depreciation. Give your answer as a percent. about 4% about 13% about 1.2% cannot be determined

Answer 1

Answer: --------- 13% -----------

Answer 2

Explanation:

We know that exponential formula of depreciation

`A=P(1-x)^t`

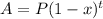
where

P is the initial amount

x is the interest rate

A is the amount after t years

we are given

The annual rate of depreciation, x, on a car that was purchased for $9,000

so, P=9000

we can plug value it

`A=9000(1-x)^t`

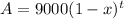
we are given

when x=5 , A=4500

so, we can plug it and solve for x

`4500=9000(1-x)^5`

`(9000\left(1-x\right)^5)/(9000)=(4500)/(9000)`

`\left(1-x\right)^5=(1)/(2)`

`x=-\left((1)/(2)\right)^{(1)/(5)}+1`

`x=0.12945`

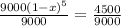
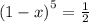
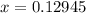
so, interest rate is 13%

now, we can plug x

and we get

`A=9000(1-0.13)^t`

`A=9000(87)^t`

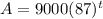
Graph: