Question

Line AB and CD have the following points: A(2, 4), B(9, 8), C(-1, 2), and D(3, -5). Are the lines parallel, perpendicular, or neither?

Perpendicular
Neither
Parallel

Answer 1

c.Parallel

Explanation:

Answer 2

We are given coordinates of A, B, C and D :

A(2, 4), B(9, 8), C(-1, 2), and D(3, -5).

Now, we need to find the slopes of AB and CD.

Slope of AB is :

`\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(2,\:4\right),\:\left(x_2,\:y_2\right)=\left(9,\:8\right)`

`m=(8-4)/(9-2)`

`m=(4)/(7)`.

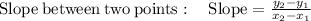
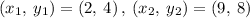
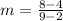
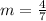Slope of CD is:

`m=(-5-2)/(3-\left(-1\right))`

`m=-(7)/(4)`.

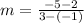
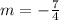Slope of CD is negative reciprocal of slope of slope of AB.

Therefore, lines AB are CD are perpendicular.