Question

What is the quotient when (x + 2) is divided into the polynomial 2x^2 - 2x - 12?

Answer 1

D

Dividing gives quotient of 2x - 6 with no remainder

Answer 2

Option: D is the correct answer.

D. The quotient is 2x-6 with no remainder.

Explanation:

We are given a polynomial as:

`2x^2-2x-12`

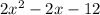
We know that any polynomial equation p(x) may be represented as:

`p(x)=q(x).s(x)+r(x)-----------(1)`

where q(x) is the quotient , s(x) is the divisor and r(x) is the remainder.

We may also represent this polynomial as follows:

`2x^2-2x-12=2(x^2-x-6)\\\\\\2x^2-2x-12=2(x^2-3x+2x-6)\\\\\\2x^2-2x-12=2(x(x-3)+2(x-3))\\\\\\2x^2-2x-12=2(x+2)(x-3)\\\\\\2x^2-2x-12=(x+2)\cdot (2(x-3))\\\\\\2x^2-2x-12=(x+2)\cdot (2x-6)`

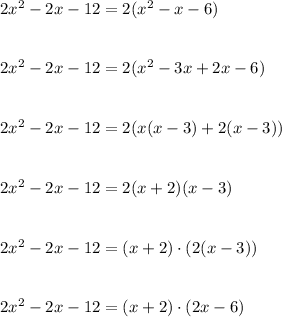
This means that on dividing the polynomial with (x+2); the quotient is: 2x-6 and remainder is zero.

( Since on comparing the equation with equation (1) )