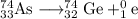Question

Arsenic-74 is a positron emitter used in locating brain tumors write an equation for this nuclear reaction and identify the product

Answer 1

`_(33)^(74)\text{As} \longrightarrow _(32)^(74)\text{Ge} + _(1)^(0)\text{e}`

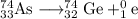
Step-by-step explanation:

The unbalanced nuclear equation is

`_(33)^(74)\text{As} \longrightarrow ? + _(1)^(0)\text{e}`

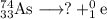
It is convenient to replace the question mark by an atomic symbol,
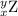`_(x)^(y)\text{Z}` , where x = the atomic number, y = the mass number, and Z = the symbol of the element .

Then your equation becomes

`_(33)^(74)\text{As} \longrightarrow _(x)^(y)\text{Z} + _(1)^(0)\text{e}`

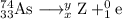
The main point to remember in balancing nuclear equations is that **the sums of the superscripts and the subscripts must be the same on each side of the equation**.

Then

74 = x + 0, so x = 74

33 = y + 1, so y = 33 -1 = 32

Element 33 is germanium, so the nuclear equation becomes

`_(33)^(74)\text{As} \longrightarrow _(32)^(74)\text{Ge} + _(1)^(0)\text{e}`