Question

An electric current in a conductor varies with time according to the expression i(t) = 110 sin (120πt), where i is in amperes and t is in seconds. what is the total charge passing a given point in the conductor from t = 0 to t = 1/180 s?

Answer 1

The total charge passing a given point in the conductor is 0.438 C.

Step-by-step explanation:

Given that,

The expression of current is

`i(t)=110\sin(120\pi t)`

`(dq(t))/(t)=110\sin(120\pi t)`

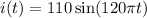
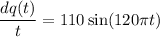
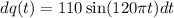`dq(t)=110\sin(120\pi t)dt`....(I)

We need to calculate the total charge

On integrating both side of equation (I)

`\int_(0)^(q)dq(t)=\int_(0)^{(1)/(180)}110\sin(120\pi t)dt`

`q=110((-\cos(120\pi t))/(120\pi))_(0)^{(1)/(180)}`

`q=-(110)/(120\pi)(cos(120\pi((1)/(180)))-\cos120\pi(0))`

`q=-0.2918(-(1)/(2)-1)`

`q=0.438\ C`

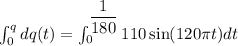
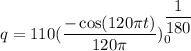
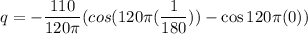
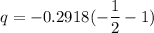
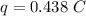
Hence, The total charge passing a given point in the conductor is 0.438 C.

Answer 2

As we know that current is defined as rate of flow of charge

`i = (dq)/(dt)`

so by rearranging the equation we can say

`q = \int i dt`

here we know that

`i(t) = 110 sin(120\pi t)`

here we will substitute it in the above equation

`q = \int 110 sin(120\pi t) dt`

`q = 110 [- (cos(120\pi t))/(120\pi)]`

now here limits of time is from t = 0 to t = 1/180s

so here it will be given as

`q = (110)/(120\pi)( -cos0 + cos((2\pi)/(3)))`

`q = 0.44 C`

so total charge flow will be 0.44 C