Answer:
The total number of possible sets is 125,000,000.
Step-by-step explanation:
3 batches of plastic tumblers are red batch, yellow batch, and purple batch.
There are 500 tumblers in each batch.
We need to make a set 3 tumblers that contain 1 tumbler of each color.
The possible ways to select r items from total n items is
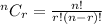
The possible ways to select 1 red tumbler from 500 tumblers red is

The possible ways to select 1 yellow tumbler from 500 tumblers yellow is

The possible ways to select 1 purple tumbler from 500 tumblers purple is

Total possible ways to make a set of 3 tumblers that contain 1 tumbler of each color are
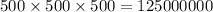
Therefore the total number of possible sets is 125,000,000.