Question

Vertices A and B of triangle ABC are on one bank of a river, and vertex C is on the opposite bank. The distance between A and B is 200 feet. Angle A has a measure of 33°, and angle B has a measure of 63°. Find b. 110 ft

168 ft
179 ft
223 ft

Answer 1

The length of side b is 179 ft

Explanation:

Given triangle ABC in which

∠A = 33°, ∠B = 63°, c=200

we have to find the length of b

In ΔABC, by angle sum property of triangle

∠A+∠B+∠C=180°

33°+63°+∠C=180°

∠C=180°-33°-63°=84°

By sine law,

`(\sin \angle A)/(a)=(\sin \angle B)/(b)=(\sin \angle C)/(c)`

`(\sin \angle B)/(b)=(\sin \angle C)/(c)`

`(\sin 63^(\circ))/(b)=(\sin 84^(\circ))/(200)`

`b=200* (\sin 63^(\circ))/(\sin 84^(\circ))=179.182887\sim 179 ft`

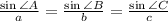
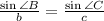
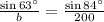
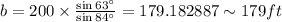
The length of side b is 179 ft

Option C is correct.