Question

The lines represented by the equations 5y – 6x = –15 and y = x + 5

are

the same line?

perpendicular?

parallel?

neither parallel nor perpendicular?

Answer 1

The lines are neither parallel nor perpendicular.

Therefore, we conclude that the statement ''neither parallel nor perpendicular'' is the correct answer.

Explanation:

The slope-intercept form of the line equation

`y = mx+b`

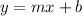
where

• m is the slope

• b is the y-intercept

Given the line equations

5y – 6x = –15

y = x + 5

Analyzing the equation 5y – 6x = –15

Given the equation

5y – 6x = –15

writing in the slope-intercept form of the line equation

5y = 6x - 15

divide both sides by 5

`y=(6)/(5)x-3`

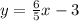
comparing with the slope-intercept form y = mx+b of the line equation

Thus, the slope of the line 5y – 6x = –15 is:

m₁ = 6/5

Analyzing the equation y = x + 5

Given the equation

y = x + 5

comparing with the slope-intercept form y = mx+b of the line equation

Thus, the slope of the line y = x + 5 is:

m₂ = 1

Conclusion:

The slope of the line 5y – 6x = –15 is:

• m₁ = 6/5

The slope of the line y = x + 5 is:

• m₂ = 1

We know that when two lines are parallel, they have equal slopes

But

m₁ ≠ m₂

6/5 ≠ 1

As the m₁ and m₂ are not equal.

Hence, the lines are NOT parallel.

We know that when two lines are parallel, the product of their slopes is -1.

Let us check the product of two slopes m₁ and m₂

m₁ × m₂ = 6/5 × 1

= 6/5

As

m₁ × m₂ ≠ -1

Thus, the lines are not perpendicular.

In a nutshell,

The lines are neither parallel nor perpendicular.

Therefore, we conclude that the statement ''neither parallel nor perpendicular'' is the correct answer.