Question

Which statement best explains the relationship between lines CD and FG?

A. They are perpendicular because their slopes are equal.
B. They are perpendicular because their slopes are negative reciprocals.
C. They are not perpendicular because their slopes are equal.
D. They are not perpendicular because their slopes are negative reciprocals.

Answer 1

B

Explanation:

ed2020

Answer 2

Two coordinates of the blue line (-4,0) and (4,2).

Let us find the slope of blue line now.

`\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-4,\:0\right),\:\left(x_2,\:y_2\right)=\left(4,\:2\right)`

`m=(2-0)/(4-\left(-4\right))`

`m=(1)/(4)`

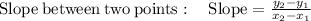
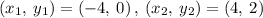
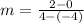
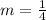
Two coordinates of the green line (-2,4) and (0,-4).

Let us find the slope of green line now.

`m=(-4-4)/(0-\left(-2\right))`

`m=-4`.

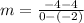
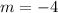We can see that slope are negative reciprocal of each other.

Therefore, correct option is B option.

B. They are perpendicular because their slopes are negative reciprocals