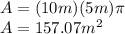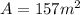Answer: 157 m²
Explanation:
1. To solve this problem you must apply the formula for calculat the area of an ellipse, which is shown below:
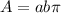
Where:
 is the distance from the center to a vertex and
is the distance from the center to a vertex and
 is the distance from the center to a co-vertex.
is the distance from the center to a co-vertex.
2. So, you have:

3. Then, you must substitute the values of
 and
and
 into the formula shown above.
into the formula shown above.
4. Therefore, you obtain that the result is: