Answer:
Explanation:
We are given that Tyler is proving that diagonal of a rectangle divides the rectangle into two triangles that have equal areas.
For that he assigned coordinates to a rectangle.
Let us assume ABCD be the rectangle with vertex A at origin that is (0,0).
And B at (l,0), C at (l,w) and D at (0,w).
Please refer the diagram attached.
Let us draw a diagonal from A to C.
So, area of the triangle formed by diagonal of rectangle = area of ΔABC
=

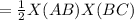
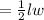
which is nothing but half of lw(area of rectangle).
Hence the area of one of the triangles formed by diagonal is half of the area of rectangle.