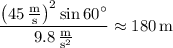The ball's horizontal position
 and vertical position
and vertical position
 at time
at time
 are given by
are given by
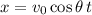
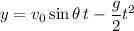
where
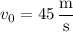 ,
,
 , and
, and
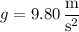 . The ball reaches the ground when
. The ball reaches the ground when
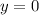 at
at
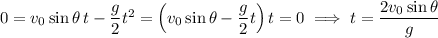
(we don't care about
 )
)
At this time, the ball's horizontal position is
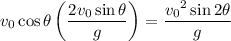
which you might recognize as the range formula. With the known parameters, the ball thus traverses a range of