Question

A researcher is testing how bacterial cells react to different environments. She placed a petri dish that initially had 32,000 bacterial cells in a vacuum chamber. One hour after being placed in the vacuum chamber, the number of cells in the petri dish had halved. Another hour later, the number of cells had again halved. The researcher creates an equation that models this pattern and can be solved to find the number of cells, y, in the dish x hours after being placed in the vacuum chamber. Plot the y-intercept of the equation and the points representing the solutions for the first three hours after the cells were placed in the vacuum chamber.I need to demonstrate it in a graph

PLEASE HELPPPP

Answer 1

(0,32000) (1, 16000) (2,8000) (3,4000)

These are the points on the graph

Hope this helps! :D

Explanation:

Answer 2

A researcher placed a petri dish with 32,000 bacterial cells. One hour after being placed in the vacuum chamber, the number of cells in the petri dish had halved. Another hour later, the number of cells had again halved.

This can be represented as exponential decreasing function,

`y=a(1 - r)^x`

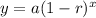
Where,

• a = starting amount = 32000
• r = rate = 50% = 0.5 as the sample becomes halved in each hour
• x = hours

Putting the values,

`\Rightarrow y=32000(1 - 0.5)^x`

`\Rightarrow y=32000(0.5)^x`

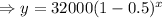
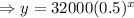
y-intercept means, where x=0, so

`\Rightarrow y=32000(0.5)^0\\\\\Rightarrow y=32000* 1=32000`

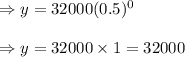
The coordinate of this poin will be (0, 32000)

This means when x=0 or at the starting of the research, the number of bacteria cells was 32000.

After 3 hours, number of bacteria cells will be,

`\Rightarrow y=32000(0.5)^3`

`\Rightarrow y=32000* 0.125`

`\Rightarrow y=4000`

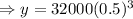
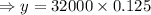
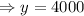
The coordinate of this point will be (3, 4000)