Question

Given:

∠3, ∠ 4 are rt. ∠'s
RS = RT

Prove:
△RZS ≅ △RZT





Which of the following lines would support the conclusion based on the given information?

RZ = RZ, Symmetric Property
RZ = RZ, Reflexive Property
TZ = ST, Perpendicular Bisector

Answer 1

RZ=RZ Reflexive Property

Step-by-step explanation:

Answer 2

the only following lines which support the conclusion based on the given information is, RZ = RZ , Reflexive Property

Step-by-step explanation:

HL (Hypotenuse Leg) theorem states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the triangles are congruent.

In ΔRZS and ΔRZT

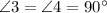`\angle 3 = \angle 4 = 90^(\circ)` [Given]

RS = RT [Hypotenuse side] [Given]

RZ = RZ [Reflexive property]

Then, by the HL theorem;

`\triangle RZS \cong \triangle RZT` Hence proved!