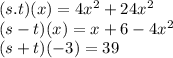Question

Suppose that the functions s and t are defined for all real numbers x as follows.

s(x)= x+6
t(x)= 4x2
write the expressions for (s.t)(x) and (s-t)(x) and evaluate (s+t)(-3).

Answer 1

`(s.t)(x) = 4x^2+24x^2\\(s-t)(x) = x+6-4x^2\\(s+t)(-3) = 39`

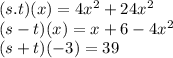
Explanation:

Given functions are:

`s(x)= x+6\\t(x)= 4x^2`

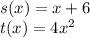
We have to find:

(s.t)(x) => this means we have to multiply the two functions to get the result.

So,

`(s.t)(x) = s(x)*t(x)\\= (x+6)(4x^2)\\=4x^2.x+4x^2.6\\=4x^3+24x^2`

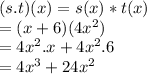
Also we have to find

(s-t)(x) => we have to subtract function t from function s

`(s-t)(x) = s(x) - t(x)\\= (x+6) - (4x^2)\\=x+6-4x^2`

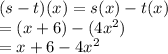
Also we have to find,

(s+t)(-3) => first we have to find sum of both functions and then put -3 in place of x

`(s+t)(x) = s(x)+t(x)\\= x+6+4x^2`

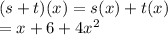
Putting x = -3

`= -3+6+4(-3)^2\\=-3+6+4(9)\\=3+36\\=39`

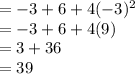
Hence,

`(s.t)(x) = 4x^2+24x^2\\(s-t)(x) = x+6-4x^2\\(s+t)(-3) = 39`