There is a formula which employs the use of determinants and which helps us calculate the area of a triangle if the vertices are given as
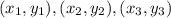 . The formula is as shown below:
. The formula is as shown below:
Area=
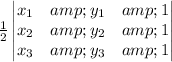
Now, in our case, we have:
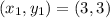
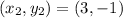 , and
, and

Thus, the area in this case will become:
Area=
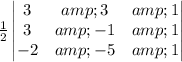
Therefore, Area=
![(1)/(2)* [[3(-1* 1-(-5)* 1]-3[3* 1-(-2)* 1]+1[3* -5-2]]= (1)/(2)* -20=-10](https://img.qammunity.org/2019/formulas/mathematics/middle-school/y51x47hj6nswaagsjglhv44dfcmkul64iq.png)
We know that area cannot be negative, so the area of the given triangle is 10 squared units.