for the system of equations
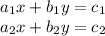
the three matrices needed to use Cramer's Rule are:
![D=\left[\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right] \\\\D_x=\left[\begin{array}{cc}c_1&b_1\\c_2&b_2\end{array}\right] \\\\D_y=\left[\begin{array}{cc}a_1&c_1\\a_2&c_2\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/c7hfogj1enu1iaiyudjiyb74yzgwpwssci.png) .
.
To use Cramer's Rule we have to calculate the three determinants listed below of the matrices listed below.
![D=\left[\begin{array}{cc}2&5\\-3&-2\end{array}\right] \\\\D_x=\left[\begin{array}{cc}-13&5\\3&-2\end{array}\right] \\\\D_y=\left[\begin{array}{cc}2&-13\\-3&3\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/m3pohkblw2gj6he9rwvcyy9gt22xw4qz63.png) .
.
The value of the determinants are shown below.
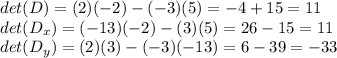
The value of y is
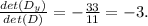 .
.