Question

How many times greater is the intensity of a 35-db sound compared to a 25-db sound?

Answer 1

10 Times (greater)

Step-by-step explanation:

The given parameters are;

The number of decibels of the first sound, 35-db

The number of decibels of the second sound, 25 db

We have;

`\beta (dB) = 10 \cdot log_(10) \left ((I)/(I_0 \right))`

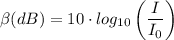
Where;

I₀ = 10⁻¹² W/m² = The lowest perceivable sound

Therefore, we have;

`I = I_0 * 10^{\left ((\beta )/(10) \right) }`

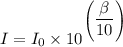
Substituting the known values, gives;

When β = 35-db, we get;

`I_(35) = 10^(-12) * 10^{\left ((35 )/(10) \right) } = 10^(-12) * 10^(3.5) = 10^(-8.5)`

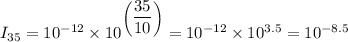
When β = 25-db, we get;

`I_(25) = 10^(-12) * 10^{\left ((25 )/(10) \right) } = 10^(-12) * 10^(2.5) = 10^(-9.5)`

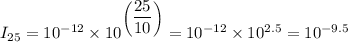
Therefore, we get the number of times the intensity of a 35-db sound is compared to a 25-db sound, which is, I₃₅/I₂₅ is given as follows;

`(I_(35))/(I_(25)) = (10^(-8.5))/(10^(-9.5)) = 10`

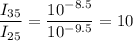
Therefore, the intensity of a 35-db sound is 10 times greater than the intensity of a 25-db sound