The correct answer is (A) 2.0 J
Total energy of the pendulum is the sum of its kinetic and potential energy. At the instant of time, when the pendulum is at a height h and has a speed v, Its energy is given by,
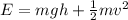
Substitute 2.0 kg for m, the mass of the pendulum, 9.81 m/s² for g, the acceleration due to gravity, 0.10 m for h and 4.0 m/s for v.

The pendulum has an initial energy of 20 J. the energy lost is given by,
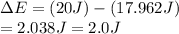
Thus, the energy lost by the pendulum is (A) 2.0 J